Introduction

Les précurseurs des télescopes astronomiques du futur sont incontestablement les deux Keck de 10 mètres de diamètre construits au sommet de la grande île d’Hawaii: leurs miroirs primaires sont composés d’une mosaïque de 36 segments hexagonaux, tous pilotés individuellement grâce à trois vérins assurant les nécessaires degrés de liberté en piston et tip-tilt. Les projets actuels des ELT américain (30 mètres) et européen (36 mètres) sont basés sur ce même principe, tandis que le successeur du télescope spatial Hubble – le James Webb Space Telescope (JWST), dont le lancement est prévu en 2014 – sera lui aussi équipé d’un miroir primaire segmenté et déployable dans l’espace. Dans tous les cas, il faudra s’assurer que les différentes facettes réfléchissantes, placées côte à côte, reconstituent effectivement la surface d’un miroir parabolique ou hyperbolique idéal, avec des discontinuités résiduelles typiquement inférieures au dixième de longueur d’onde: on dit alors que tous les miroirs sont cophasés. Pour ce faire, les ingénieurs et les chercheurs doivent inventer de nouvelles méthodes de réglage. Mais la technique de cophasage ne se limite pas aux seuls télescopes géants: elle est également fondamentale sur les interféromètres à ouvertures séparées, terrestres ou spatiaux et capables d’atteindre des résolutions spatiales extrêmes. Il faut alors concevoir une nouvelle génération de Senseurs de surface d’onde (SSO) capables de mesurer les pistons différentiels entre les diverses sections – éventuellement non jointives – de la surface optique collectrice, car les SSO actuels de type Shack-Hartmann, à courbure ou pyramidal semblent peu adaptés à cette tâche. Ce constat est à l’origine d’une réflexion personnelle engagée depuis bientôt cinq années au CRAL, puis à l’OCA, et qui m’a progressivement amené vers un nouveau concept de SSO en plan image et à décalage de phase répondant aux principales exigences résumées plus haut.

Top | Version PDF | Retour HDR | Références

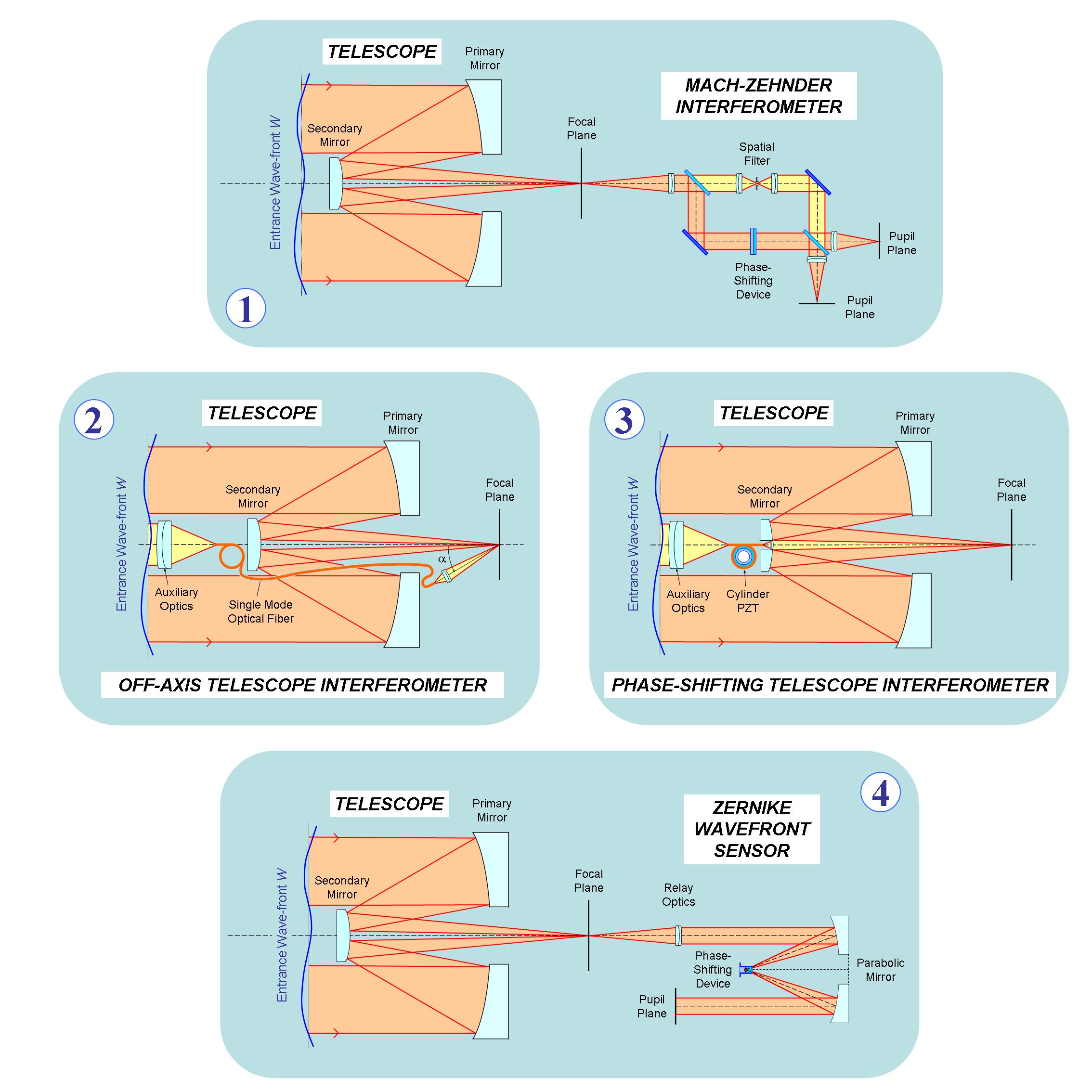
Principe du senseur de surface d’onde à décalage de phase

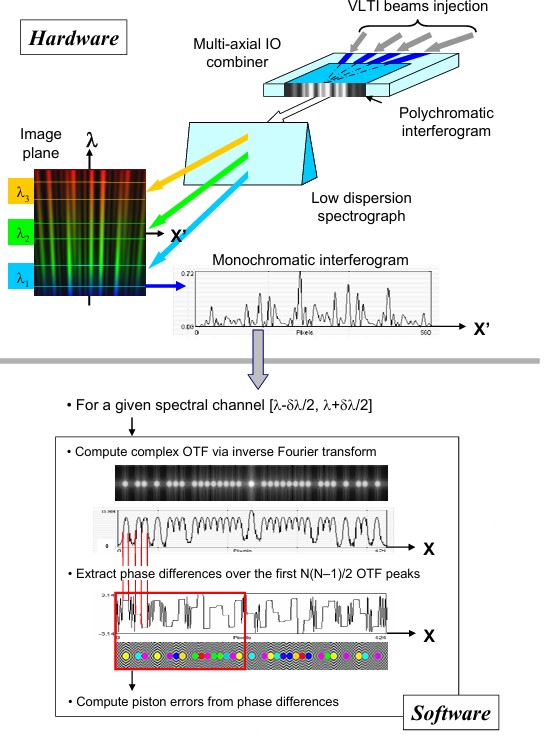
Le principe actuel du SSO à décalage de phase (également appelé “Télescope-Interféromètre” dans les premières publications) peut être résumé dans les deux schémas ci-dessous [1-2]: il consiste à introduire un déphasage connu et variable dans le temps sur l’une des facettes réflectrices du télescope, dénommée “facette de référence”, puis à tirer parti des modifications constatées sur l’image d’une étoile non résolue afin d’en déduire des informations précises sur l’état de cophasage des segments. En pratique, il sera plus commode d’introduire un piston équivalent sur un miroir mobile optiquement conjugué avec la surface optique géante en cours d’examen.

Principe du senseur de surface d’onde à décalage de phase (à gauche) et systèmes de coordonnées utilisés pour le télescope segmenté et son plan focal (à droite)

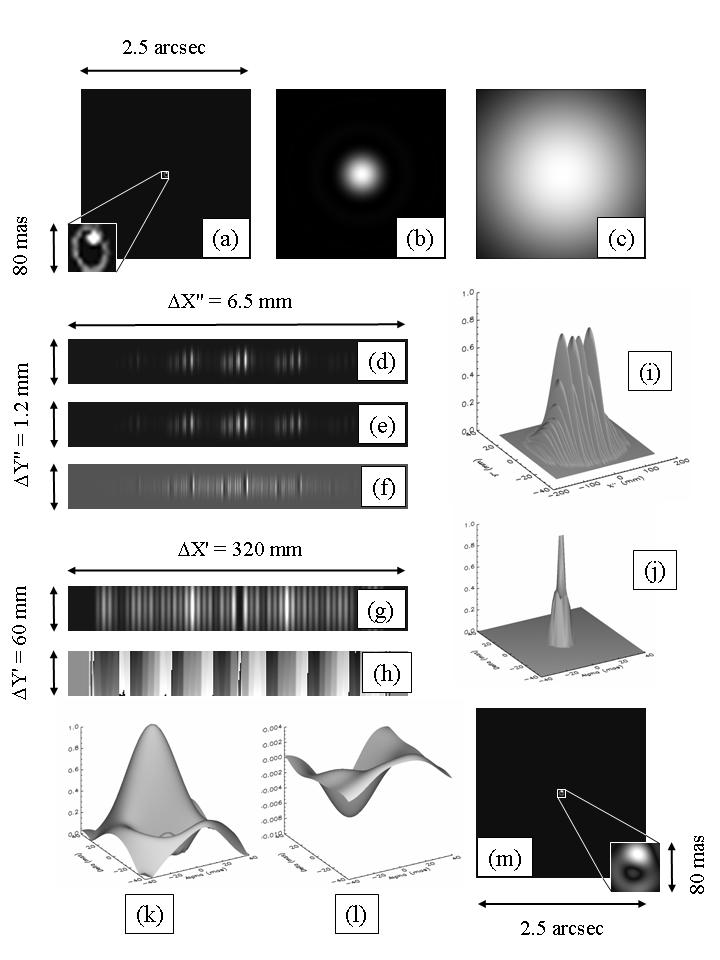
Après avoir introduit le déphasage sur la facette de référence, on mesure la réponse impulsionnelle du télescope (plus connue par son abréviation anglaise PSF, pour Point Spread Function) dans le plan image O’X’Y’ en utilisant par exemple une matrice CCD. Puis on calcule la Fonction de Transfert Optique (FTO en anglais) de l’ensemble du système au moyen d’une transformation de Fourier inverse, qui nous ramène dans le plan pupille OXY. Les principales étapes du procédé sont résumées sur la figure ci-dessous.

Principales étapes de reconstruction du front d'onde

Les simulations numériques sont effectuées avec le logiciel COSAC et confirment que le procédé est efficace, rapide d’exécution et applicable sur les télescopes segmentés du futur fonctionnant dans un régime d’optique adaptative [3]. Une question importante porte sur le bien-fondé de “l’approximation Delta” qui définit la résolution spatiale du dispositif et limite l’ouverture de la sous-pupille de référence: pour un télescope terrestre, celle-ci ne devrait en principe pas excéder le rayon de Fried r₀. Cette question a été étudiée dans les références [3] et [4]. On montre notamment que la première version du télescope-interféromètre où la sous-pupiille de référence est située loin de l'axe optique [5] est moins favorable, car le facteur de contraste y est plus faible et les erreurs de mesure de la phase amplifiées en conséquence. La figure ci dessous montre l’évolution de l’erreur de mesure du front d'onde en fonction du diamètre de la pupille de référence rapporté à celui de l’ELT, de la magnitude de l’étoile guide, des conditions atmosphériques et du type de SSO (avec ou sans décalage de phase). Dans le cas d’un télescope de 30 mètres, l’erreur de mesure du SSO à décalage de phase reste inférieure à la limite de diffraction tant que la magnitude de l’étoile guide n’excède pas 8 par moyennes conditions de seeing (r₀ = 0.25 m), et 11 dans de bonnes conditions (r₀ = 0.5 m). On en déduit que la technique est particulièrement bien adaptée à un futur instrument chasseur de planètes extrasolaires opérant dans l’infrarouge.

Erreurs de mesure du senseur de surface d’onde en fonction de divers paramètres. A gauche, les diamètres de l’ELT et de la pupille de référence.
A droite, la magnitude de l’étoile guide et les conditions atmosphériques pour un ELT de 30 mètres de diamètre

Les développements potentiels de la méthode sont nombreux: mesures multispectrales pour étendre la plage de mesure des pistons différentiels, capacité d’évaluation des erreurs de tip-tilt et de la scintillation atmosphérique, étude d’un procédé de déconvolution rapide pour passer outre “l’approximation Delta”, etc. Ces travaux permettent de progresser sur la voie des senseurs de surface d’onde de nouvelle génération en plan image. Le développement le plus récent de la méthode de décalage de phase est résumé dans la section suivante, où le principe est étendu en mode multi-couleurs.

Top | Version PDF | Retour HDR | Références

Extension à trois longueurs d’onde

La méthode décrite dans la section précédente est en principe applicable à toutes les surfaces optiques segmentées, qu’il s’agisse d’interféromètres à ouvertures séparées ou des futurs télescopes extrêmement grands (ELT) destinés à succéder aux Keck ou au VLT dans le courant de la prochaine décennie. Dans une récente publication [6], j’ai tenté d’étendre la plage de mesure de cette méthode aux erreurs de piston différentiel très importantes qui affectent couramment les télescopes ou interféromètres terrestres. Par rapport aux SSO “classiques” de type Shack-Hartmann, à courbure ou pyramidal, le senseur de surface d’onde à décalage de phase présente l’avantage d’effectuer des mesures de front d'onde directes, sans passer par des données intermédiaires telles les dérivées premières ou secondes de la surface d’onde. En contrepartie la plage de mesure est limitée par la longueur d'onde l du rayonnement électro-magnétique considéré. C'est une indétermination intrinsèque de la méthode que l’onappelle souvent “ambiguïté de 2p” qui veut que la mesure reste toujours comprise entre –0.5l et +0.5l tandis que la partie entière du front d'onde demeure inconnue.
Cette ambiguïté peut être levée de différentes manières, et l’a été ici au moyen d’une technique multi-spectrale de “longueur d’onde synthétique” inspirée des méthodes de mesure de distance sans contact par interférométrie multi couleurs. Elle consiste à combiner les mesures effectuées à trois longueurs d’onde différentes pour obtenir un système de 3N équations à 4N inconnues, admettant a priori une infinité de solutions. On montre pourtant que le système admet un jeu unique de solutions dans l’intervalle [-l_S, +l_S] où l_S est la “longueur d’onde synthétique” définie par la relation:

Il suffit alors d’ajuster le triplet des longueurs d’onde de mesure pour couvrir l’ensemble du domaine de variation des erreurs de piston que l’on souhaite corriger. Outre une proposition de design instrumental basé sur un spectrographe intégral de champ, la référence [5] présente une validation de l’ensemble du concept effectuée au moyen de plusieurs séries de simulations numériques: la modélisation des PSF polychromatiques enregistrées sur le détecteur a été réalisée avec le logiciel COSAC, tandis que l’ensemble des traitements algorithmiques a été programmé sous IDL (incluant notamment les transformations de Fourier inverses, les extractions de phase et leur dépliage sur les trois longueurs d’onde). Les résultats typiques de ces simulations sont illustrés ci-dessous pour un triplet de longueurs d’onde visibles égal à 0.45 µm, 0.50 µm et 0.55 µm avec diverses largeurs de bandes spectrales

Mesure des erreurs de cophasage d’un télescope segmenté en large bande spectrale [5]


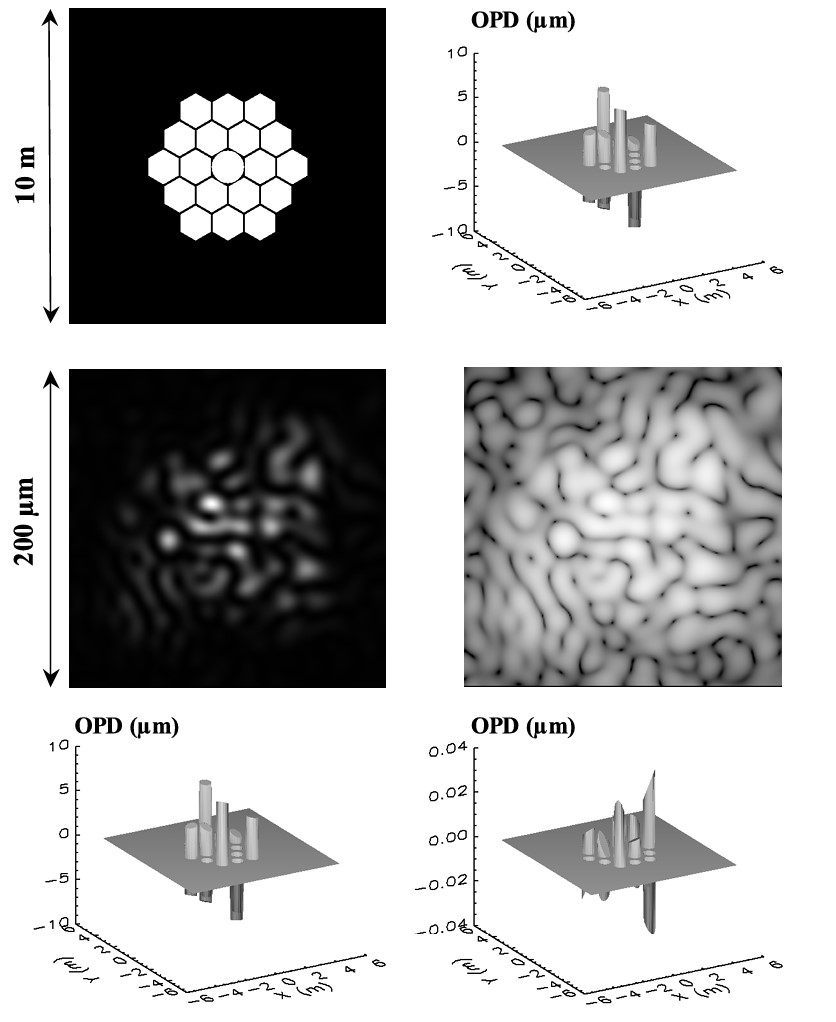
	De gauche à droite et de bas en haut: carte de transmission dans la pupille (avec une sous-pupille de référence centrale et circulaire), vue 3D des erreurs de phase initiales (écarts PTV = 15.5 µm et RMS = 4.6 µm), représentation en niveau de gris de la PSF du télescope dans le plan image (échelles linéaire et logarithmique), vue 3D de la surface d’onde reconstruite, et carte des différences entre les erreurs initiales et mesurées (écarts PTV = 71 nm et RMS = 14 nm)		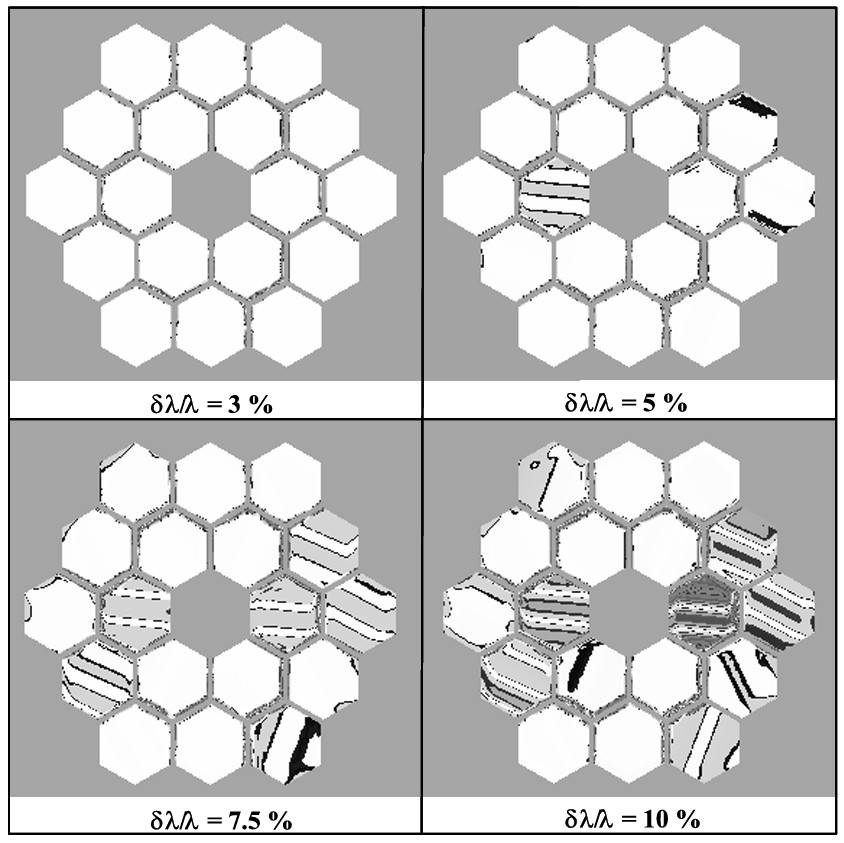Simulations effectuées pour les trois longueurs d’onde de référence. Chacune des 18 facettes hexagonales de ce télescope de 6.5 mètres de diamètre inspiré du JWST est affectée d’erreurs en piston et en tip-tilt tirées aléatoirement sur des intervalles de +/- 10 micron et +/- 1 microradian respectivement. Les erreurs de mesure sont codées sur une échelle de gris où le blanc correspond à des valeurs inférieures à 10 nm et le noir à des valeurs supérieures à 1 µm

Les simulations numériques montrent que les valeurs exactes des désalignements d’origine sont correctement déterminées sur la plupart des facettes hexagonales (zones représentées en blanc), et que leur surface totale diminue de manière inversement proportionnelle à la largeur spectrale. Mais la méthode multi-spectrale fait preuve ici d’une robustesse remarquable, puisqu’elle permet d’éliminer en temps réel les fausses estimations par comparaison des trois valeurs de piston obtenues pour chaque longueur d’onde. Il reste ainsi possible de réaliser d’excellentes mesures de piston et de tip-tilt, même lorsque les “zones de confiance” à la surface d’une facette réflectrice sont limitées aux zones blanches en haut et à droite. Dans sa version multi-spectrale, le senseur de surface d’onde à décalage de phase est donc susceptible d’atteindre les précisions de cophasage requises pour le mode imagerie des ELT et des futurs réseaux de télescopes, qui sont typiquement de l’ordre de l/10 PTV. La méthode a été mise en oeuvre avec succès le banc de test SIRIUS de l’OCA [7] et proposée dans le cadre du projet POPS, senseur de franges de deuxième génération du VLTI [8].

Top | Version PDF | Retour HDR | Références

Activités post-HDR

Elles n'ont pas vraiment leur place ici, mais je tenais à les évoquer brièvement par quelques références bibliographiques et figures:

[9] Application à un interféromètre stellaire imageur
[10] Application à un suiveur de franges pour le VLTI
[11] Applications en coronographie


	Interféromètre stellaire imageur	Suiveur de franges	Coronographie

Top | Version PDF | Retour HDR | Références

Références

	[1]	F. Hénault, “Conceptual design of a phase shifting telescope-interferometer,” Optics Communications vol. 261, p. 34-42 (2006)
	[2]	F. Hénault, “Telescope interferometers: an alternative to classical wavefront sensors,” Proceedings of the SPIE vol. 7015, n° 70151X (2008)
	[3]	F. Hénault, “Signal-to-noise ratio of phase sensing telescope interferometers,” J. Opt. Soc. Am. A vol. 25, p. 631-642 (2008)
	[4]	F. Hénault, “Un senseurde surface d’ondeen plan image et àdécalagede phase,” Atelier Télescopes spatiaux de nouvelle génération, CNES Toulouse (27-28 mars 2012)
	[5]	F. Hénault, “Analysis of stellar interferometers as wavefront sensors,” Applied Optics vol. 44, p. 4733-4744 (2005)
	[6]	F. Hénault, “Multi-spectral piston sensor for co-phasing giant segmented mirrors and multi-aperture interferometric array,” Journal of Optics A: Pure Applied Optics vol. 11, n° 125503 (2009)
	[7]	N. Tarmoul, D. Mourard, F. Hénault, J.-M. Clausse, P. Girard, A. Marcotto, N. Mauclert, A. Spang, Y. Rabbia, A. Roussel, “Implementation of the Chromatic Phase Diversity method on the SIRIUS test bench,” Proceedings of the SPIE vol. 7734, n° 773428 (2010)
	[8]	N. Tarmoul, F. Hénault, D. Mourard, J.-B. Le Bouquin, L. Jocou, P. Kern, J.-P. Berger, O. Absil, “Multi-axial integrated optics solution for POPS, a 2nd-generation VLTI fringe tracker,” Proceedings of the SPIE vol. 7734, n° 773425 (2010)
	[9]	F. Hénault, “Phase-shifting technique for improving the imaging capacity of sparse-aperture optical interferometers,” Applied Optics vol. 50, p. 4207-4220 (2011)
	[10]	F. Hénault, “Phase-shifting fringe tracking method for sparse aperture interferometer arrays,” Proceedings of the SPIE vol. 8445, n° 84452U (2012)
	[11]	F. Hénault, A. Carlotti, C. Vérinaud, “Phase-shifting coronagraph,” Proceedings of the SPIE vol. 10400, n° 104001J (2017)

Top | Version PDF | Retour HDR | Références